clarke 正变换
通俗点讲就是将难以控制的电机三相,降维投影到两个坐标轴,缩减控制变量。
复杂的三相变化问题就降解为了α-β坐标轴的坐标上的数值变化问题。
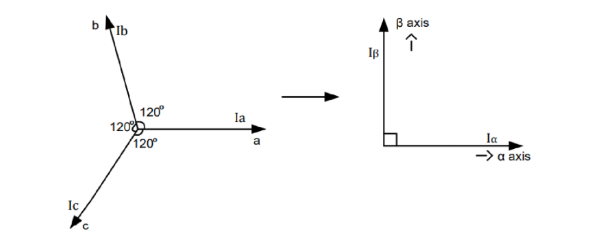
利用三角函数进行投影: 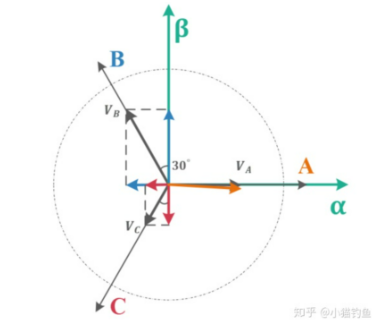
显然,针对α-β坐标系中α轴,有:
针对α-β坐标系中β轴,有:
把上面的投影结果列成矩阵形式,有:
但是这个式子并不是最终的投影式,之后需要添加幅值的系数,原因如下:
用
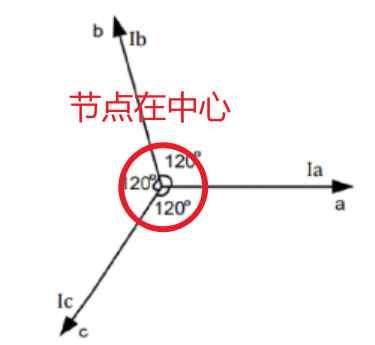
设
将
由于 b,c 相电流投影的存在,导致在 a 相输入
因此,为了让式子等辐值,即使得 a 相
基于等赋值变换,就能够得到 α、β 相位与
代入:
根据基尔霍夫电流定律:
进一步的,可求
根据基尔霍夫电流定律:
最终可以得到:
clarke 逆变换
将
根据基尔霍夫电流定律推导出
最终得到: