二叉树
二叉树的存储方式
二叉树可以链式存储,也可以顺序存储。
那么链式存储方式就用指针, 顺序存储的方式就是用数组。
顾名思义就是顺序存储的元素在内存是连续分布的,而链式存储则是通过指针把分布在散落在各个地址的节点串联一起。
链式存储如图:
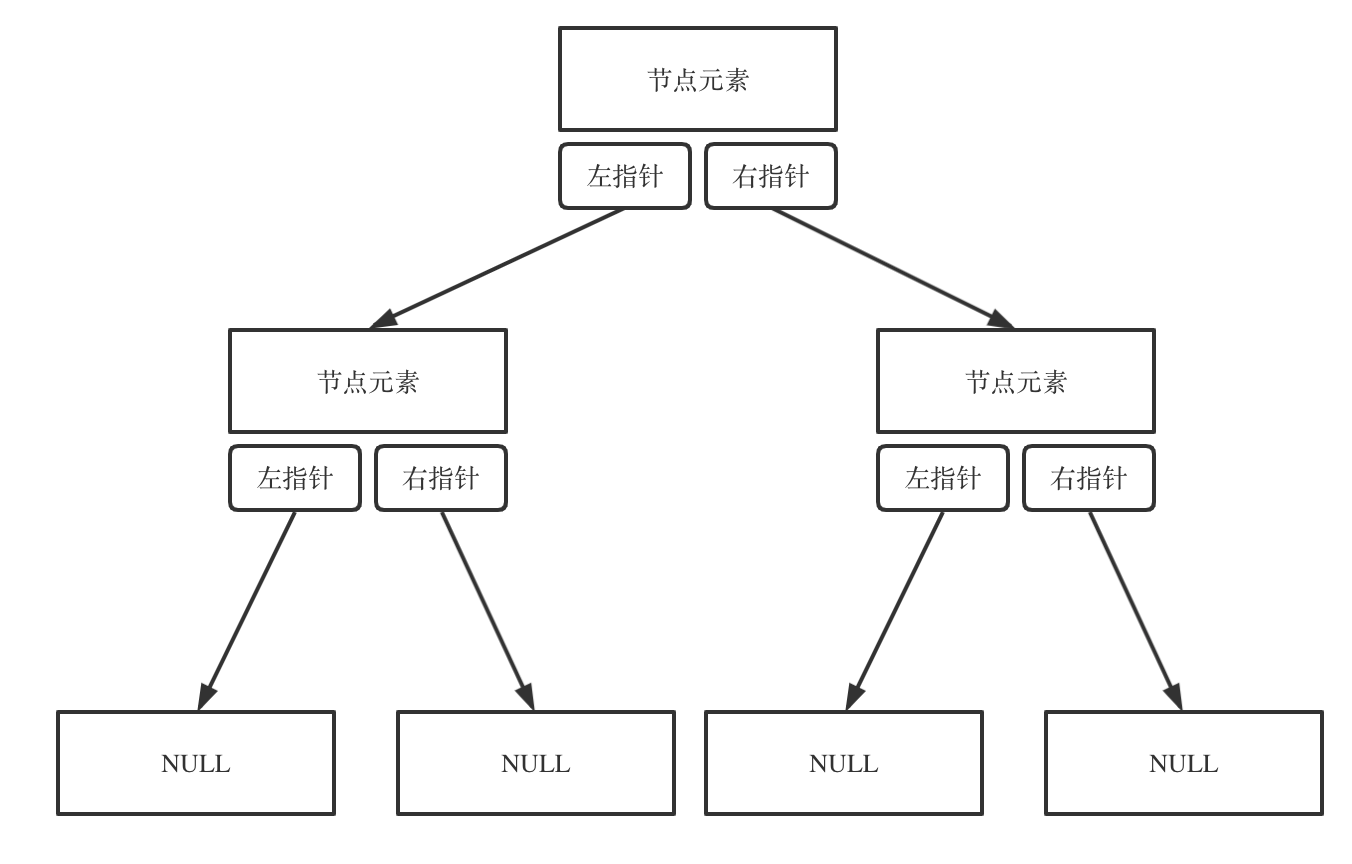
链式存储是大家很熟悉的一种方式,那么我们来看看如何顺序存储呢?
其实就是用数组来存储二叉树,顺序存储的方式如图:
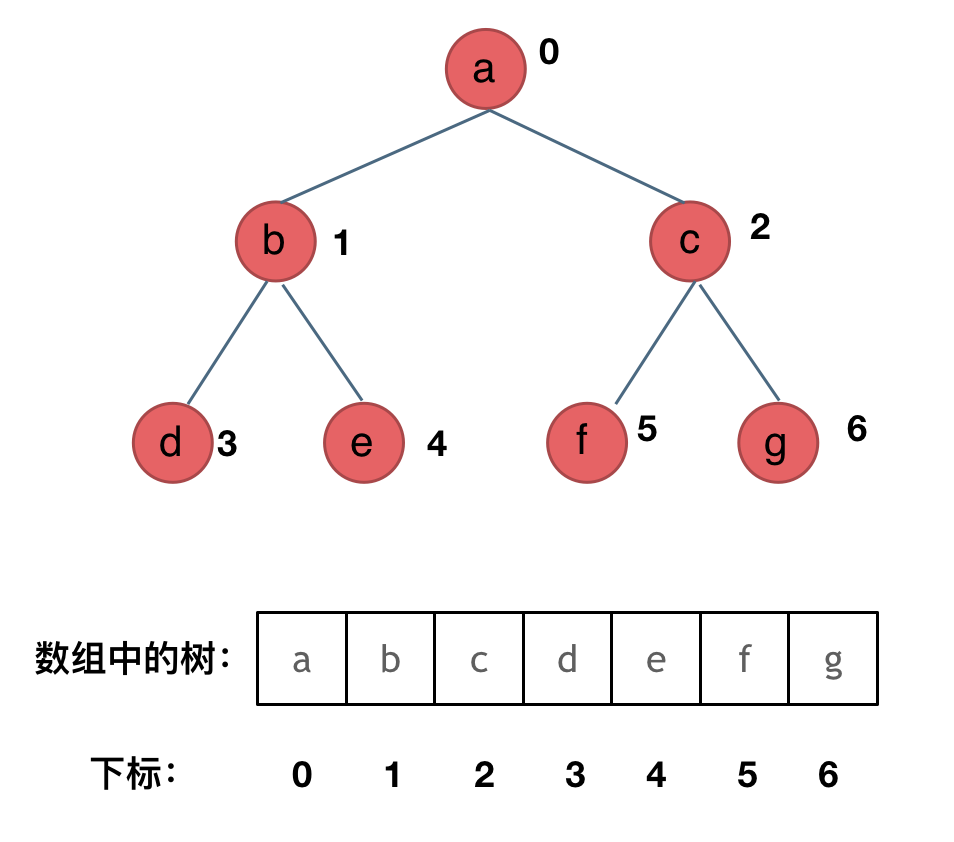
用数组来存储二叉树如何遍历的呢?
如果父节点的数组下标是 i,那么它的左孩子就是 i * 2 + 1,右孩子就是 i * 2 + 2。
但是用链式表示的二叉树,更有利于我们理解,所以一般我们都是用链式存储二叉树。
二叉树种类
满二叉树
满二叉树:如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。
完全二叉树
完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2^(h-1) 个节点。
二叉搜索树
二叉搜索树是一个有序树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树
平衡二叉搜索树
平衡二叉搜索树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
定义
c++
struct TreeNode{
int val;
TreeNode* left;
TreeNode* right;
TreeNode(val): val(val), left(NULL), right(NULL) {}
};
c
typedef struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
}* PNode, TNode;
PNode initNode(int val) {
PNode tree = (PNode) malloc(sizeof(TNode));
tree->val = val;
tree->left = NULL;
tree->right = NULL;
return tree;
}
js
class TreeNode {
val;
left;
right;
constructor(val = 0, left = null, right = null) {
this.val = val;
this.left = left;
this.right = right;
}
}
java
class TreeNode {
private val;
private TreeNode left;
private TreeNoee right;
TreeNode () {}
TreeNode (int val) {
this.val = val;
}
TreeNode (int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
二叉树的递归遍历
前序遍历
c++
void traversal(TreeNode* cur, vector<int>& num) {
if(cur == NULL) return;
//根节点
num.push_back(cur->val);
//左子树
traversal(cur->left, num);
//右子树
traversal(cur->right, num);
}
vector<int> preorderTraversal(TreeNode* tree) {
//定义结果数组
vector<int> result;
traversal(tree, result);
return result;
}
中序遍历
//左子树
traversal(cur->left, num);
//根节点
num.push_back(cur->val);
//右子树
traversal(cur->right, num);
后序遍历
//左子树
traversal(cur->left, num);
//右子树
traversal(cur->right, num);
//根节点
num.push_back(cur->val);
c
前序
void traversal(PNode tree, int* res, int* resLen) {
if(tree === NULL) return ;
res[(*resLen) ++] = tree->val;
traversal(tree->left, res, resLen);
traversal(tree->right, res, resLen);
}
int* preorder(PNode tree) {
int* res = (int *) malloc(sizeof(100));
traversal(tree, res, 0);
return res;
}
js
function preorder(tree) {
let res = [];
function traversal (tree) {
if(!tree) return ;
res.push(tree.val);
traversal(tree.left);
traversal(tree.right);
}
traversal(tree);
return res;
}
二叉树的迭代遍历
前序遍历
c++
vector<int> preorderTraversal(TreeNode* tree) {
vector<int> result;
//使用栈来存储节点
stack<TreeNode*> st;
//前序遍历先储存根节点
st.push(tree);
while(! st.empty()) {
TreeNode* cur = st.top();
//将根节点的值放入结果数组中
result.push_back(cur->val);
st.pop();
//入栈时先右后左,出栈则为先左后右
if(cur->right) st.push(cur->right);
if(cur->left) st.push(cur->left);
}
return result;
}
c
int* preorder(PNode tree) {
// 构建结果数组
int* res = (int *) malloc(sizeof(100));
int resLen = 0;
// 构建结构体指针数组
PNode stackNodes[100] = {tree};
int stackTop = 1;
while(stackTop != 0) {
PNode cur = stackNodes[-- stackTop];
res[resLen ++] = cur->val;
//入栈时先右后左,出栈则为先左后右
if(cur->right != NULL) stackNodes[stackTop ++] = cur->right;
if(cur->left != NULL) stackNodes[stackTop ++] = cur->left;
}
return res;
}
js
function preorder(tree) {
let res = [];
let stack = [tree];
while(stack.length != 0) {
let cur = stack[stack.length --];
res.push(cur.val);
if(cur.right != null) stack.push(cur.right):
if(cur.left != null) stack.push(cur.left);
}
return res;
}
java
public int[] preorder(TreeNode tree) {
List<Integer> res = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
stack.push(tree);
while(! stack.isEmpty()) {
TreeNode cur = stack.top();
res.add(cur.val);
if(cur.left != null) stack.push(cur.left);
if(cur.right != null) stack.push(cur.right);
}
return res.stream().mapToInt(Integer::valueOf).toArray();
}
中序遍历
c++
//思路是先把所有的左子树存入栈
vector<int> InorderTraversal(TreeNode* tree) {
vector<int> result;
stack<TreeNode*> st;
TreeNode* cur = tree;
while(cur != NULL || ! st.empty()) {
//判断是否到最后一个左子树
if(cur != NULL) {
st.push(cur);
cur = cur->left;
}else {
//获取最后一个左子树
cur = st.top();
st.pop();
result.push_back(cur->val);
//遍历所有左子树最近的右子树
cur = cur->right;
}
}
return result;
}
c
int* inorder(PNode tree) {
int* res = (int *) malloc(sizeof(100));
int resLen = 0;
PNode stackNodes[100] = (PNode) malloc(sizeof(PNode) * 100);
int stackTop = 0;
PNode cur = tree;
// 在栈中放入所有左子树
while(cur != NULL || stackTop != 0) {
if(cur != NULL) {
stackNodes[stackTop ++] = cur;
cur = cur->left;
}else {
// 当最左边的左子树记录后,栈中推入最近右子树
cur = stackNodes[-- stackTop];
res[resTop ++] = cur->val;
// 需要判断NULL值,所以不判断是否为NULL
cur = cur->right;
}
}
return res;
}
js
function inorder(tree) {
int res = [];
int stack = [];
TreeNode cur = tree;
while(cur || stack.length) {
if(cur) {
stack.push(cur);
cur = cur.left;
}else {
cur = stack[stack.length --];
res.push(cur->val);
cur = cur-right;
}
}
return
}
java
public int[] inorder(TreeNode tree) {
List<Integer> res = new ArrayList();
Stack<TreeNode> stack = new stack<>();
TreeNode cur = tree;
while(cur != null || stack.isEmpty()) {
if(cur != null) {
stack.push(cur);
cur = cur.left;
}else {
cur = stack.top();
stack.pop();
res.add(cur.val);
cur = cur.right;
}
}
return res.stream().mapToInt(Integer::valueOf).toArray();
}
后序遍历
先序遍历是中左右,后续遍历是左右中,那么我们只需要调整一下先序遍历的代码顺序,就变成中右左的遍历顺序,然后在反转result数组,输出的结果顺序就是左右中了
vector<int> postorderTraversal(TreeNode* tree) {
vector<int> result;
//使用栈来存储节点
stack<TreeNode*> st;
//前序遍历先储存根节点
st.push(tree);
while(! st.empty()) {
TreeNode* cur = st.top();
//将根节点的值放入结果数组中
result.push_back(cur->val);
st.pop();
//入栈时先左后左,出栈则为先右后左
if(cur->left) st.push(cur->left);
if(cur->right) st.push(cur->right);
}
// 翻转结果数组
reverse(result.begin(), result.end());
return result;
}
二叉树的统一迭代法
更换顺序完成前中后的遍历
中序遍历
c++
vector<int> inorderTraversal(TreeNode* tree) {
vector<int> result;
stack<TreeNode*> st;
if(tree != NULL) st.push(tree);
while(!st.empty()) {
TreeNode* cur = st.top();
if(cur != NULL) {
// 弹出栈顶元素避免重复
st.pop();
// 中序遍历一次放入右,中,左
// 不为空再放入栈中
if(cur->right) st.push(cur->right);
// 放入根节点
st.push(cur);
// 用 NULL 作为标识来表示已经访问过根节点
st.push(NULL);
// 放入左子树
if(cur->left) st.push(cur->left);
//为空表示所有节点遍历完成
}else {
// 弹出NULL
st.pop();
cur = st.top();
st.pop();
result.push_back(cur->value);
}
}
return result;
}
c
int* inorder(PNode tree) {
int* res = (int *) malloc(sizeof(100));
int resTop = 0;
PNode stackNodes[100] = (PNode) malloc(sizeof(PNode));
int stackTop = 0;
stackNodes[stackTop ++] = tree;
while(stackTop != 0) {
// 弹出防止重复,因为后面又放了一次根节点
PNode cur = stackNodes[-- stackTop];
stackTop --;
if(cur != NULL) {
// 中序遍历右中左
if(cur->right != NULL) stackNodes[stackTop ++] = cur->right;
// 作为节点需要添加一个标识
stackNodes[stackTop ++] = cur;
stackNodes[stackTop ++] = NULL;
// 左子树作为栈顶
if(cur->left != NULL) stackNodes[stackTop ++] = cur->left;
}else {
// 上面已经弹出了一个元素NULL
cur = stackNodes[-- stackTop];
res[resTop ++] = cur->val;
}
}
return res;
}
js
function inorder(tree) {
let res = [];
let stack = [tree];
while(stack.length != 0) {
TreeNode cur = stack[stack.length --];
if(cur) {
if(cur.right) stack.push(cur.right);
stack.push(cur);
stack.push(null);
if(cur.left) stack.push(cur.left);
}else {
cur = stack[stack.length --];
res.push(cur.val);
}
}
return res;
}
java
public int[] inorder(TreeNode tree) {
List<Integer> res = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
stack.push(tree);
while(! stack.isEmpty()) {
TreeNode cur = stack.pop();
if(cur) {
if(cur.right) stack.push(cur.right);
stack.push(cur);
stack.push(null);
if(cur.left) stack.push(cur.left);
}else {
cur = stack.pop();
res.add(cur.val);
}
}
return res.stream().mapToInt(Integer::valueOf).toArray();
}
后序遍历
vector<int> postorderTraversal(TreeNode* tree) {
vector<int> result;
stack<TreeNode*> st;
if(tree != NULL) st.push(tree);
while(! st.empty()) {
TreeNode* cur = st.top();
if(cur != NULL) {
//后序遍历先放入根节点
st.pop();
st.push(cur);
st.push(NULL);
if(cur->right) st.push(cur->right);
if(cur->left) st.push(cur->left);
}else {
//删除 NULL
st.pop();
cur = st.top();
result.push_back(cur->val);
st.pop();
}
}
}
二叉树的层序遍历
c++
迭代法
vector<vector<int>> levelOrder(TreeNode* tree) {
//构建一个队列来遍历每一层
queue<TreeNode*> que;
vector<vector<int>> result;
if(tree != NULL) que.push(tree);
while(!que.empty()) {
//构建每一层的容器
vector<int> res;
//计算每一层的数量
int size = que.size();
for(int i = 0; i < size; i ++) {
TreeNode* cur = que.front;
res.push_back(cur->val);
que.pop();
if(cur->right) que.push(cur->right);
if(cur->left) que.push(cur->left);
}
result.push_back(res);
}
return result;
}
递归法(DFS 深度优先)
class Solution {
public:
void order(TreeNode* tree, vector<vector<int>> result, int deepth) {
if(tree == nulptr) return ;
// 按照深度构建出每一层
if(result.size() == deepth) result.push_back(vector<int>());
result[deepth].push_back(tree->val);
order(tree->left, result, deepth ++);
order(tree->right, result, deepth ++);
}
vector<vector<int>> levelOrder(TreeNode tree) {
int deepth = 0;
vector<vector<int>> res;
order(tree, res, deepth);
return result;
}
}
js
function levelOrder(tree) {
let result = new Array(new Array(0));
let queue = new Array();
queue.unshift(tree);
while(queue.length) {
let len = queue.length;
let res = new Array();
for(let i = 0; i < len; i ++) {
let cur = queue.pop();
res.push(cur->val);
if(cur->left) queue.unshift(cur->left);
if(cur->right) queue.unshift(cur->right);
}
result.push(res);
}
return result;
}
// 递归
function levelOrder(tree) {
let result = new Array(new Array(0));
let deepth = 0;
function order(tree, deepth) {
if(!tree) return ;
if(result.length == deepth) result.push(new Array());
result[deepth].push(tree->val);
order(tree->left, deepth ++);
order(tree->right, deepth ++);
}
return result;
}
java
public class Solution {
private List<List<Integer>> result = new ArrayList<List<Integer>>;
// 迭代法
public List<List<Integer>> levelOrder(TreeNode tree) {
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(tree);
while(!queue.isEmpty()) {
List<Integer> res = new ArrayList<Integer>();
int size = queue.size();
while(size) {
TreeNode cur = queue.poll();
res.add(cur.val);
if(cur.left) queue.offer(cur.left);
if(cur.right) queue.offer(cur.right);
}
result.add(res);
}
return result;
}
// 递归法
public List<List<Integer>> levelOrder(TreeNode tree) {
List<List<Integer>> result = new ArrayList<>();
order(tree, result, 0);
return result;
}
public void order(TreeNode tree, List<List<Integer>> result, int deepth) {
if(tree == null) return ;
if(result.size() == deepth) {
List<Integer> list = new ArrayList<>();
result.get(deepth).push(list);
}
list.push(tree.val);
order(tree.left, result, deepth ++);
order(tree.right, result, deepth ++);
}
}
翻转二叉树
递归
c++
TreeNode* reverseTree(TreeNode* tree) {
if(tree == NULL) return tree;
swap(tree->right, tree->left);
reverseTree(tree->left);
reverseTree(tree->right);
return tree;
}
迭代法
在前中后遍历时将结果数组的代码替换为
swap(cur->left, cur->right);
c
PNode reverseTree(TreeNode* tree) {
if(tree == NULL) return tree;
swap(tree->left, tree->right);
reveseTree(tree->left);
reveseTree(tree->right);
return tree;
}
js
function reverseTree(tree) {
if(!tree) return tree;
swap(tree.left, tree.right);
reverseTree(tree.left);
reveseTree(tree.right);
return tree;
}
java
public TreeNode reverseTree(TreeNode tree) {
if(!tree) return tree;
swap(tree.left, tree.right);
reverseTree(tree.left);
reverseTree(tree.right);
return tree;
}
对称二叉树
给定一个二叉树,检查它是否是镜像对称的
c++
递归法
bool compare(TreeNode* left, TreeNode* right) {
if(left == NULL && right == NULL) return true;
else if(left != NULL && right == NULL) return false;
else if(left == NULL && right != NULL) return false;
else if(left->val != right->val) return false;
bool outside = compare(left->left, right->right);
bool inside = compare(left->right, right->left);
return outside && inside;
}
bool isSymmetric(TreeNode* tree) {
if(tree == NULL) return true;
//判断二叉树是否对称,只需要判断根节点的左右子树是否对称
return compare(tree->left, tree->right);
}
迭代法
bool isSymmetric(TreeNode* tree) {
//使用队列来逐个判断子树是否对称(使用其他数据结构也可以)
queue<TreeNode*> que;
if(tree == NULL) return true;
que.push(tree->left);
que.push(tree->right);
while(!que.empty()) {
TreeNode* left = que.front(); que.pop();
TreeNode* right = que.front(); que.pop();
if(left == NULL && right == NULL) {
continue;
}
if(!left || !right || (left->val != right->val)) {
return false;
}
que.push(left->left);
que.push(right->right);
que.push(left->right);
que.push(right->left);
}
return true;
}
c
// 递归法
int compare(PNode left, PNode right) {
if(left == NULL && right == NULL) return 1;
if(left != NULL || right != NULL || (left->val != right->right)) return -1;
// 外层的节点
int outside = compare(left->left, right->right);
// 内层的节点
int inside = compare(left->right, right->left);
if(outside == -1 || inside == -1) return -1;
return 1;
}
// 迭代法
int compare(PNode tree) {
if(tree == NULL) return 1;
PNode stackNodes[100] = (PNode) malloc(sizeof(PNode));
int stackTop = 0;
stackNodes[stackTop ++] = tree->right;
stackNodes[stackTop ++] = tree->left;
while(stackTop != 0) {
PNode left = stackNodes[-- stackTop];
PNode right = stackNodes[-- stackTop];
if(left == NULL && right == NULL) continue;
if(left != NULL || right != NULL || (left->val != right->right)) return -1;
}
return 1;
}
js
// 递归法
function compare(left, right) {
if(!left && !right) return true;
if(!left || !right || (left.val != right.val)) return false;
return compare(left.left, right.right) && compare(left.right, right.left);
}
// 迭代法
function compare(tree) {
int stack = [];
stack.push(tree);
while(stack.length) {
let left = stack.pop();
let right = stack.pop();
if(!left && !right) continue;
if(!left || !right || (left.val != right.val)) return false;
stack.push(left.left);
stack.push(right.right);
stack.push(left.right);
stack.push(left.left);
}
return true;
}
java
// 递归法
public bool compare(TreeNode left, TreeNode right) {
if(left == null && right == null) return true;
if(left != null || right != null || (left.val != right.val)) return false;
return compare(left.left, right.right) && compare(left.right, right.left);
}
// 迭代法
public bool compare(TreeNode tree) {
if(!tree.left && !tree.right) return true;
Stack<TreeNode> stack = new Stack<>();
stack.push(tree.left);
stack.push(tree.right);
while(!stack.isEmpty()) {
TreeNode left = stack.pop();
TreeNode right = stack.pop();
if(left == null && right == null) continue;
if(left || right || (left.val != right.val)) return false;
stack.push(left.left);
stack.push(right.right);
stack.push(left.right);
stack.push(right.left);
}
return true;
}
二叉树的最大深度
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
c++
递归
int getDepth(TreeNode* tree) {
if(tree == NUll) return 0;
return 1 + max(getDepth(tree->left), getDepth(tree->right));
}
前序遍历
class Solution {
public:
int result;
void getDepth(TreeNode* tree, int depth) {
result = result > depth ? result : depth;
if(tree->left == NULL && tree->right == NULL) return;
if(tree->left) {
getDepth(tree->left, depth + 1);
}
if(tree->rigth) {
getDepth(tree->right, depth + 1);
}
return ;
}
int getMax(TreeNode* tree) {
int result = 0;
if(tree == NULL) return result;
getDepth(tree, 1);
return result;
}
}
迭代法的层序遍历
int getDepth(TreeNode* tree) {
int depth = 0;
queue<TreeNode*> que;
que.push(tree);
while(! que.empty()) {
int size = que.size();
depth ++;
for(int i = 0; i < size; i ++) {
TreeNode* cur = que.front();
que.pop();
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
}
return depth;
}
js
// 递归法
function getDepth(tree) {
if(!tree) return 0;
return 1 + Math.max(getDepth(tree.left), getDepth(tree.right));
}
// 递归前序遍历
function getDepth(tree) {
if(!tree) return 0;
let result = 0;
function getD(tree, depth) {
result = result > depth ? result : depth;
if(!tree.left && !tree.right) return ;
if(tree.left) getD(tree.left, depth + 1);
if(tree.right) getD(tree.right, depth + 1);
return ;
}
getD(tree, 1);
}
// 迭代层序遍历
function getDepth(tree) {
let depth = 0;
let queue = [];
queue.unshift(tree);
while(queue.length) {
int len = queue.length;
depth ++;
while(len) {
TreeNode cur = queue.pop();
if(cur.left) queue.unshift(cur.left);
if(cur.right) queue.unshift(cur.right);
}
}
return depth;
}
java
// 迭代法
public int getDepth(TreeNode tree) {
if(!tree) return 0;
return 1 + Math.max(getDepth(tree.left), getDepth(tree.right));
}
// 前序迭代法
class Solution {
private int result = 0;
public void getDepth(TreeNode tree, int depth) {
result = result > depth ? result : depth;
if(!tree.left && !tree.right) return ;
if(tree.left) getDepth(tree.lefet, depth + 1);
if(tree.right) getDepth(tree.right, depth + 1);
}
}
//
N叉树的最大深度
c++
递归法
int maxDepth(TreeNode* tree) {
if(tree == NULL) return 0;
int depth = 0;
for(int i = 0; i < tree->children.size(); i ++) {
depth = max(depth, maxDepth(tree->chidren[i]));
}
return depth + 1;
}
迭代法
层序遍历
int maxDepth(TreeNode* tree) {
int depth = 0;
queue<int> que;
que.push(tree);
while(! que.empty()) {
int size = que.size();
depth ++;
for(int i = 0; i < size; i ++) {
TreeNode* cur = que.front();
que.pop();
for(int j = 0; j < cur->children.size(); j ++) {
if(que.children[j]) que.push(cur->children[j]);
}
}
}
return depth;
}
二叉树的最小深度
最小深度是从根节点到最近叶子节点的最短路径上的节点数量
递归法
int getMinDepth(TreeNode* tree) {
if(tree == NULL) return 0;
if(tree->left == NULL && tree->right! = NULL) {
return 1 + getMinDepth(tree->right);
}
if(tree->left != NULL && tree->right == NULL) {
return 1 + getMinDepth(tree->left);
}
return 1 + min(getMinDepth(tree->left), getMinDepth(tree->rigth));
}
迭代法
层序遍历
int getMinDepth(TreeNode* tree) {
if(tree == NULL) return 0;
queue<TreeNode*> que;
int depth = 0;
que.push(tree);
while(! que.empty()) {
int size = que.size();
depth ++;
for(int i = 0; i < size; i ++) {
TreeNode* cur = que.front();
que.pop();
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
//当左右子树都为空的时候则为最小深度
if(! cur->left && ! cur->right) {
return depth;
}
}
}
return depth;
}
完全二叉树的节点数
普通二叉树
递归法
int countNode(TreeNode* tree) {
if(tree == NULL) return 0;
return conutNode(tree->left) + countNode(tree->right) + 1;
}
迭代法
//层序遍历
int count;
for(;i < size;) count ++;
完全二叉树
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
–> 判断一个左子树或者右子树是不是满二叉树
在完全二叉树中,如果递归向左遍历的深度等于递归向右遍历的深度,那说明就是满二叉树
int countNodes(TreeNode* tree) {
if(tree == NULL) return 0;
TreeNode* left = tree->left;
TreeNodse* right = tree->right:
int leftCount = 0, rightCount = 0;
//完全二叉树中,左子树的数量若等于右子树的数量则说明是满二叉树,可以根据公式计算节点数量
while(left) {
left = left->left;
leftCount ++;
}
while(right) {
right = right->right;
rightCount ++;
}
if(leftCount == rightCount) {
//(2 ^ h) - 1
return (2 << leftCount) - 1;
}
//若不为满二叉树,则寻找子树的满二叉树
return countNodes(tree->left) + countNodes(tree->right) + 1;
}
平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
class Solution {
public:
int getHeight(TreeNode* node) {
if(node == NULL) return 0;
//若递归时返回 -1 则都返回 -1
int leftH = getHeight(node->left);
if(leftH == -1) return -1;
int rightH = getHeight(node->right);
if(rightH == -1) return -1;
//若相差大于1,则说明不为平衡二叉树, 或者返回深度
return abs(leftH - rightH) > 1 ? -1 : max(leftH, rightH);
}
bool isBalanced(TreeNode* tree) {
return getHeight(tree);
}
}
二叉树的所有路径
这道题目要求从根节点到叶子的路径,所以需要前序遍历,这样才方便让父节点指向孩子节点,找到对应的路径。
在这道题目中将第一次涉及到回溯,因为我们要把路径记录下来,需要回溯来回退一个路径再进入另一个路径。
前序遍历以及回溯的过程如图:
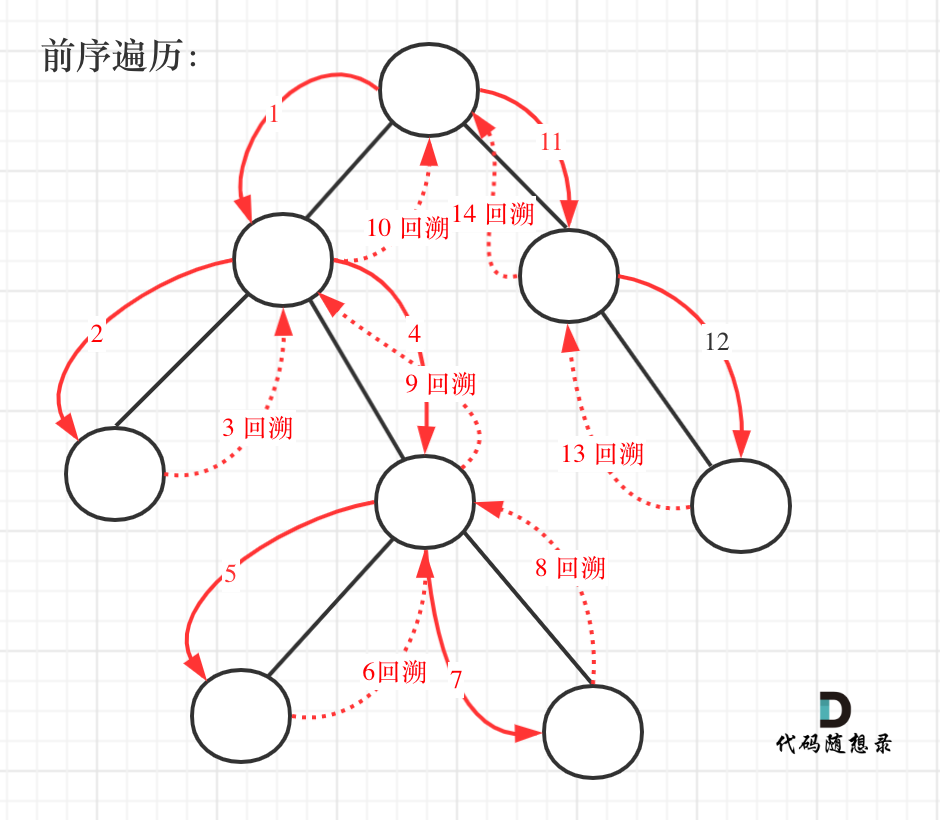
我们先使用递归的方式,来做前序遍历。要知道递归和回溯就是一家的,本题也需要回溯。
class Solution {
public:
void traversal(TreeNode* node, vector<int> path, vector<string> result) {
//通过不断的递归,将路径的值写入容器
path += to_string(node->val);
//递归的终止条件,遍历到叶子节点则回溯上一个,延展到其他路径
if(node->left == NULL && node->right == NULL) {
//将路经以 val -> val 写入
string paths;
//最后一个元素另外写入
for(int i = 0; i < path.size() - 1; i ++) {
paths += to_string(path[i]);
paths += "->";
}
paths += to_string(path[path.size() - 1]);
result.push_back(paths);
return ;
}
//左子树的路径记录
if(node->left) {
traversal(node->left, path, result);
//进行回溯,上一代码有结果后,删除一个节点以更改路径
path.pop_back();
}
if(node->right) {
traversal(node->right, path, result);
path.pop_back();
}
}
vector<string> binaryTreePaths(TreeNode* tree) {
vector<string> result;
vector<int> path;
traversal(tree, path, result);
return result;
}
}
左叶子之和
int sumOfLeftLeaves(TreeNode* tree) {
if(tree == NULL) return 0;
if(tree->left == NULL && tree->right) return 0;
//递归左子树
int leftValue = sumOfLeftLeaves(tree->left);
//如果有左子树且左子树的左右都为空,则为叶子节点
if(tree->left && !tree->left->left && !tree->right->right) {
leftValue = tree->left->val;
}
//递归右子树
int rightValue = sumOfLeftLeaves(tree->right);
return leftValue + rightValue;
}
迭代法(前)
int sumOfLeftLeaves(TreeNode* tree) {
if(tree == NULL) return 0;
int result = 0;
stack<TreeNode*> st;
st.push(tree);
while(! st.empty()) {
TreeNode* cur = st.top();
st.pop();
if(cur->left && !cur->left->left && !cur->left->right) {
result += cur->left->val;
}
if(cur->left) st.push(cur->left);
if(cur->right) st.push(cur->right);
}
return result;
}
找树左下角的值
给定一个二叉树,在树的最后一行找到最左边的值。
递归法
class Solution {
public:
int result;
int maxDepth = MAX_DEPTH;
//使用 depth 来递归深度
void traversal(TreeNode* node, int depth) {
if(tree == NULL) return 0;
//找到叶子节点则执行最终逻辑
if(tree->left == NULL && tree->right == NULL) {
if(depth > maxDepth) {
maxDepth = depth;
result = node->val;
}
return ;
}
//左子树
if(tree->left) {
depth ++;
traversal(node->left, depth);
//进行回溯到上一个节点,往下进行递归,需要回溯来找最大深度
depth --;
}
//右子树
if(tree->right) {
depth ++;
traversal(node->right, depth);
depth --;
}
return ;
}
int findBottomLeftValue(TreeNode* tree) {
int depth = 0;
traversal(tree, depth);
return result;
}
}
迭代法
层序遍历
int findBottomLeftValue(TreeNode* tree) {
if(tree == NULL) return 0;
int result = 0;
queue<TreeNode*> que;
que.push(tree);
while(! que.empty()) {
int size = que.size();
for(int i = 0; i < size; i ++) {
TreeNode* cur = que.front();
que.pop();
if(i == 0) result = cur->val;
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
}
return result;
}
路径总和
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
bool
递归
bool traversal(TreeNode* node, int sum) {
//如果遍历到叶子节点,并且sum 为 0 的时候说明存在路径
if(!node->left && !node->right && sum == 0) return true;
//否则不存在
if(!node->left && !node->right) return false;
if(node->left) {
sum -= node->left->val;
traversal(node->left, sum);
//回溯到上一节点,将减去的值恢复
sum += node->left->val;
}
if(node->right) {
/*
隐藏回溯
traversal(node->rigth, sum - node->val);
*/
sum -= node->right->val;
traversal(node->right, sum);
//回溯到上一节点,将减去的值恢复
sum += node->right->val;
}
return false;
}
bool hasPathSum(TreeNode* tree, int sum) {
if(tree == NULL) return 0;
return traversal(tree, sum);
}
迭代
在栈中保存一个容器,容器包含当前节点以及路径到此节点相加的值
bool hasPathSum(TreeNode* tree, int sum) {
if(tree == NULL) return 0;
stack<pair<TreeNode*, int>> st;
st.push(pair<TreeNode*, int> (tree, 0));
while(! st.empty()) {
pair<TreeNode*, int> node = st.top();
st.pop();
//判断叶子节点来执行
if(!node.first->left && !node.first->right && sum = node.second) return true;
//遍历左子树和右子树
if(node.first->left) {
st.push(pair<TreeNode*, int> (node.first->left, node.second + node.first->left.val));
}
if(node.first->right) {
st.push(pair<TreeNode*, int> (node.first->right, node.second + node.second->right.val));
}
return false;
}
}
路径总和 ii
计算出所有相加为 sum 的路径并放在结果数组
递归法
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void traversal(TreeNode* node, int count) {
//判断为叶子节点执行
if(!node->left && !node->right && count == 0) {
result.push_back(path);
return ;
}
if(!node->left && !node->right) return;
//左右子树遍历
if(node->left) {
count -= node->left->val;
path.push_back(node->left->val);
traversal(node->left, count);
//回溯
count += node->val;
path.pop();
}
if(node->right) {
count -= node->right->val;
path.push_back(node->right->val);
traversal(node->rigth, count);
//回溯
count += node->right->val;
path.pop();
}
return ;
}
vector<vector<int>> pathSum(TreeNode* tree, int sum) {
if(tree == NULL) return;
traversal(tree, sum);
return result;
}
}
从中序和后序遍历构建二叉树
就是以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来再切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
流程如图:
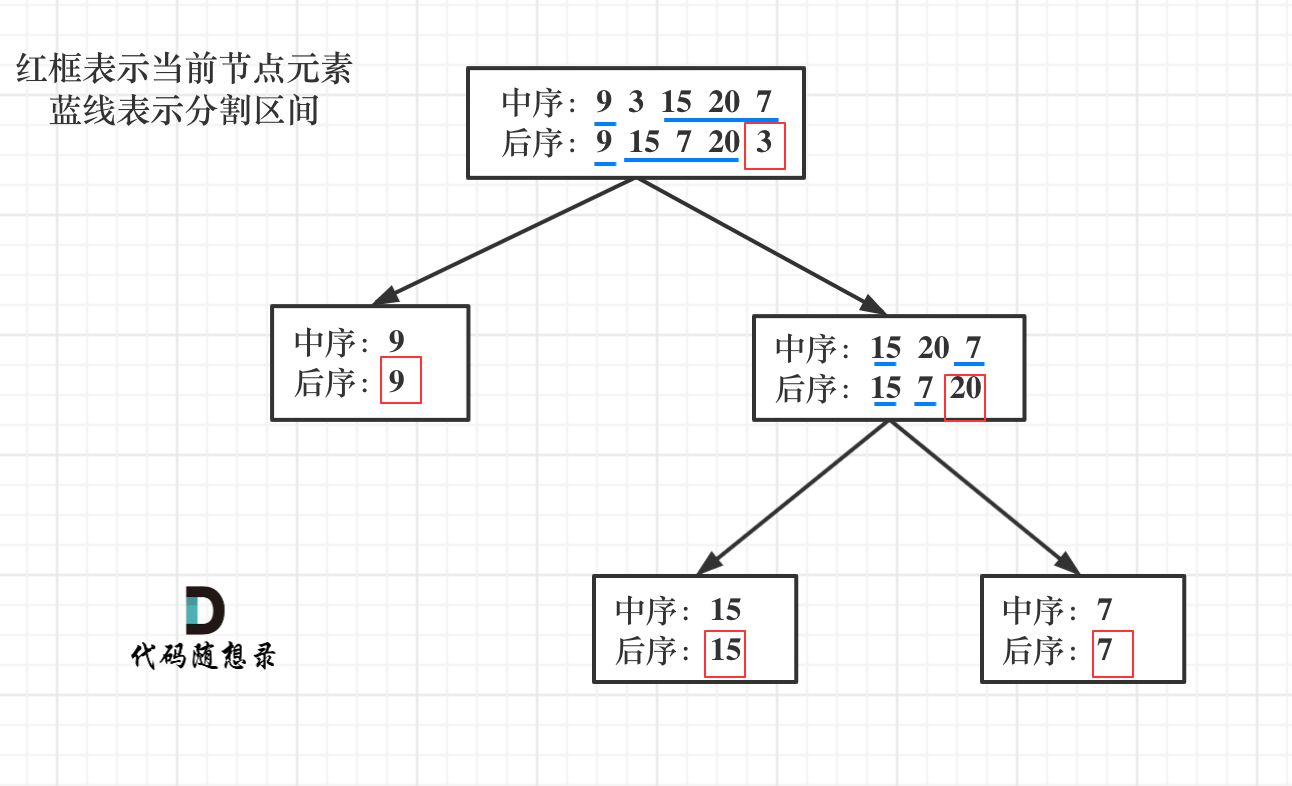
说到一层一层切割,就应该想到了递归。
来看一下一共分几步:
- 第一步:如果数组大小为零的话,说明是空节点了。
- 第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
- 第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
- 第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
- 第五步:切割后序数组,切成后序左数组和后序右数组
- 第六步:递归处理左区间和右区间
class Solution {
TreeNode* traversal(vector<int> inorder, vector<int> postorder) {
//设定终止条件
if(inorder.size() == 0) return NULL;
//让后序遍历的最后一个节点作为根节点
int rootValue = postorder[postorder.size() - 1];
//创建一个新节点
TreeNode* tree = new TreeNode(rootValue);
//以后序数组的最后一个元素为界,分割前序数组
int delimiterInorder;
for(delimiterInorder = 0; delimiterInorder < inorder.size(); delimiterInorder ++) {
if(inorder[delimiterInorder] == rootValue);
}
//开始切割前序数组
//左前序数组[0, delimiterInorder)
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterInorder);
//右前序数组[delimiterInorder + 1, inorder.end);
vector<int> rightInorder(delimiterInorder + 1, inorder.end());
//后序数组删除最后一位,重新定义内存
postorder.resize(postorder.size() - 1);
//用前序数组切割后序数组
//左后序数组
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
//进行左子树递归
tree->left = traversal(leftInorder, leftPostorder);
//右子树递归
tree->right = traversal(rightInorder, rightPostorder);
return tree;
}
TreeNode* buildTree(vector<int> inorder, vector<int> postorder) {
if(inorder.size() == 0 || postorder.size() == 0) return NULL;
return traversal(inorder, postorder);
}
}
优化版
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd)
// 切割中序数组
// 左中序区间,左闭右开[leftInorderBegin, leftInorderEnd)
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
// 右中序区间,左闭右开[rightInorderBegin, rightInorderEnd)
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// 切割后序数组
// 左后序区间,左闭右开[leftPostorderBegin, leftPostorderEnd)
int leftPostorderBegin = postorderBegin;
int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size
// 右后序区间,左闭右开[rightPostorderBegin, rightPostorderEnd)
int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素,已经作为节点了
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, postorder, leftPostorderBegin, leftPostorderEnd);
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);
前序遍历和后序遍历构造二叉树
// 切割中序数组
// 中序左区间,左闭右开[leftInorderBegin, leftInorderEnd)
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
// 中序右区间,左闭右开[rightInorderBegin, rightInorderEnd)
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// 切割前序数组
// 前序左区间,左闭右开[leftPreorderBegin, leftPreorderEnd)
int leftPreorderBegin = preorderBegin + 1;
int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size
// 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)
int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
int rightPreorderEnd = preorderEnd;
最大二叉树
给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下:
- 二叉树的根是数组中的最大元素。
- 左子树是通过数组中最大值左边部分构造出的最大二叉树。
- 右子树是通过数组中最大值右边部分构造出的最大二叉树。
通过给定的数组构建最大二叉树,并且输出这个树的根节点。
class Solution {
public:
TreeNode* traversal(vector<int> nums, int left, int right) {
if(right >= left) return nullptr;
int maxValueIndex = left;
for(int i = left + 1; i < right; i ++) {
if(nums[i] > nums[maxValueIndex]) maxValueIndex = i;
}
//创建新的节点,值为数组的最大值
TreeNode* tree = new TreeNode(nums[maxValueIndex]);
//表示区间[nums.begin(), maxValueIndex)
int leftNum = nums.begin() + maxValueIndex;
int rightNum = maxValueIndex + 1;
//节点的左子树
tree->left = traversal(nums, nums.begin(), nums.begin() + maxValueIndex);
//节点右子树
tree->right = traversal(nums, maxValueIndex + 1, nums.end());
return tree;
}
TreeNode* constructMaximumBinaryTree(vector<int> nums) {
return traversal(nums, 0, nums.size());
}
}
合并二叉树
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
递归法
//更改t1的结构
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if(t1 == NULL) return t2;
if(t2 == NULL) return t1;
t1->val += t2->val;
t1->left = mergeTrees(t1->left, t2->left);
t2->right = mergeTree(t1->right, t2->right);
return t1;
}
//重新构建一个二叉树
TreeNode* mergeTrees(TreeNode* t1, TreeNode * t2) {
if(t1 == NULL) return t1;
if(t2 == NULL) return t2;
TreeNode* tree = new TreeNode(0);
tree->val = t1->val + t2->val;
tree->left = mergeTrees(t1->left, t2->left);
tree->right = mergeTrees(t1->right, t2->right);
return tree;
}
迭代法
TreeNode* mergeTree(TreeNode* t1, TreeNode* t2) {
if(t1 == NULL) return t1;
if(t2 ==NULL) return t2;
queue<TreeNode*> que;
que.push(t1);
que.push(t2);
while(! que.empty()) {
TreeNode* tree1 = que.front(); que.pop();
TreeNode* tree2 = que.front(); que.pop();
tree1->val += tree2->val;
if(tree1->left != NULL && tree2->left != NULL) {
que.push(tree1->left);
que.push(tree2->left);
}
if(tree1->right != NULL && tree2->right != NULL) {
que.push(tree1->right);
que.push(tree2->right);
}
if(tree1->left != NULL && tree2->left == NULL) {
tree1->left = tree1->left;
}
if(tree1->right == NULL && tree2->right != NULL) {
tree1->right = tree2->right;
}
}
return tree1;
}
使用指针直接更改树
void traversal(TreeNode** t1, TreeNode** t2) {
if((*t1) == NULL && (*t2) == NULL) return ;
if((*t1) != NULL && (*t2) != NULL) {
(*t1)->val += (*t2)->val;
}
if((*t1) != NULL && (*t2) == NULL) {
return ;
}
if((*t1) == NULL && (*t2) != NULL) {
*t1 = *t2;
}
traversal((*t1)->left, (*t2)->left);
traversal((*t1)->right, (*t2)->right);
}
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if(t1 == NULL && t2 == NULL) return NULL;
//传递引用,形参就为指针的指针
traversal(&t1, &t2);
return t1;
}
二叉搜索树的搜索
因为二叉搜索树的节点是有序的,所以可以有方向的去搜索。
如果root->val > val,搜索左子树,如果root->val < val,就搜索右子树,最后如果都没有搜索到,就返回NULL
递归法
TreeNode* searchBST(TreeNode* node, int val) {
if(node == NULL && node->val == val) return node;
if(node->val > val) return searchBST(node->left, val);
if(node->val < val) return searchBST(node->right, val);
return NULL;
}
迭代法
TreeNode* searchBST(TreeNode* tree, int val) {
while(tree != NULL) {
if(tree->val > val) {
tree = tree->left;
}else if(tree->val < val) {
tree = tree->right;
}else {
return tree;
}
}
return NULL;
}
验证二叉搜索树
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
递归法
class Solution {
public:
vector<int> result;
void traversal(TreeNode* node) {
if(node == NULL) return ;
//遍历到最左边的叶子节点
traversal(node->left);
//从后往前开始记录
result.push_back(node->val);
traversal(node->right);
}
bool isBST(TreeNode* tree) {
if(tree == NULL) return false;
traversal(tree);
//判断结果数组是否有序递增,有序说明是搜索树
for(int i = 0; i < result.size(); i ++) {
if(result[i] < result[i - 1]) return false;
}
return true;
}
}
递归法2
利用不断遍历,寻找有序的最大值,有序则代表搜索树合理
long long MaxValue = LONG_INT;
bool isVaildBST(TreeNode* tree) {
if(tree == NULL) return ;
//中序遍历
bool left = isVaildBST(tree->left);
if(MaxValue < tree->val) MaxValue = tree->val;
else return false;
//右子树
bool right = isVaildBST(tree->right);
return left && right;
}
迭代法
bool isVaildBST(TreeNode* tree) {
stack<TreeNode*> st;
TreeNode* cur = tree;
TreeNode* pre = NULL;
while(cur != NULL && ! st.empty()) {
if(cur != NULL) {
st.push(cur);
cur = cur->left;
}else {
cur = st.top();
st.pop();
//若当前的节点的值小于前一个节点,说明不是有序递增
if(pre != NULL && cur->val <= pre->val) return false;
//记录当前节点作为前一个节点
pre = cur;
cur = cur->right;
}
}
return true;
}
二叉搜索树的最小绝对差
给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。
递归法
中序遍历
class Solution {
public:
vector<int> vec;
void traversal(TreeNode* tree) {
if(tree == NULL) return;
if(tree->left) traversal(tree->left);
result.push_back(tree->val);
if(tree->right) traversal(tree->right);
}
int getMinimumDifference(TreeNode* tree) {
traversal(tree);
if(vec.size() < 2) return ;
int result = INT_MAX;
for(int i = 0; i < vec.size(); i ++) {
result = min(result, vec[i] - vec[i - 1]);
}
return result;
}
}
递归法2
记录前一个节点,与当前节点做比对
class Solution {
public:
int result = INT_MAX;
TreeNode* pre = NULL;
void traversal(TreeNode* tree) {
if(tree == NULL) return ;
traversal(tree->left);
if(pre != NULL) {
result = min(result, tree->val - pre->val);
}
pre = tree;
traversal(tree->right);
}
int getMinimumDifference(TreeNode* tree) {
if(tree == NULL) return;
traversal(tree);
return result;
}
}
迭代法
int getMinimumDifference(TreeNode* tree) {
stack<TreeNode*> st;
TreeNode* cur = tree;
TreeNode* pre = NULL;
int result = INT_MAX;
while(cur != NULL || ! st.empty()) {
if(cur != NULL) {
st.push(cur);
st.pop();
cur = cur->left;
}else {
cur = st.top();
if(pre != NULL) {
result = min(result, cur->val - pre->val);
}
pre = cur;
cur = cur->rigth;
}
}
return result;
}
二叉搜索树的众数
给定一个有相同值的二叉搜索树(BST),找出 BST 中的所有众数(出现频率最高的元素)。
假定 BST 有如下定义:
- 结点左子树中所含结点的值小于等于当前结点的值
- 结点右子树中所含结点的值大于等于当前结点的值
- 左子树和右子树都是二叉搜索树
如果不是二叉搜索树
- 这个树都遍历了,用map统计频率
- 把统计的出来的出现频率(即map中的value)排个序
要把map转化数组即vector,再进行排序,当然vector里面放的也是pair<int, int>类型的数据,第一个int为元素,第二个int为出现频率。
3. 取前面高频的元素
class Solution {
private:
//递归遍历节点,将节点的值和频率存储在map中
void traversal(TreeNode* node, unorder_map map) {
if(node == NULL) return ;
map[node->val] ++;
traversal(node->left);
traversal(node->right);
}
//定义排序方式
bool cmp(const pair<int, int>& a, const pair<int, int>& b) {
//升序排序
return a.second > b.second;
}
public:
vector<int> findMode(TreeNode* tree) {
vector<int> result;
unorder_map<int, int> map;
if(tree == NULL) return result;
traversal(tree, map);
vector<pair<int, int>> vec(map.begin(), map.end());
//进行排序
sort(vec.begin(), vec.end(), cmp);
result.push_back(vec[0].first);
for(int i = 0; i < vec.size(); i ++) {
if(vec[i].second == vec[0].second)
result.push_back(vec[i]);
}
return result;
}
}
如果是二叉搜索树
class Solution {
private:
int count = 0;
int maxCount = 0;
TreeNode* cur = NULL;
vector<int> result
//中序遍历
void traversal(TreeNode* tree) {
if(tree == NULL) return ;
//左
traversal(tree->left);
//中
if(pre == NULL) {
count = 1;
}else if(pre->val == tree->val) {
count ++;
}else {
count = 1;
}
pre = cur;
if(count == maxCount) {
result.push_back(tree->val);
}
if(count > maxCount) {
maxCount = count;
result.clear();
result.push_back(tree->val);
}
//右
traversal(tree->right);
return ;
}
public:
vector<int> findMode(TreeNode* tree) {
count = 0;
maxCount = 0;
TreeNode* pre = NULL;
result.clear();
traversal(tree);
return result;
}
}
迭代法
vector<int> findMode(TreeNode* tree) {
int count = 0;
int maxCount = 0;
TreeNode* cur = tree;
vector<int> result;
stack<int> st;
//中序遍历
while(cur != NULL && ! st.empty()) {
if(cur != NULL) {
st.push(cur);
cur = cur->left;
}else {
cur = st.top();
st.pop();
if(tree == NULL) return ;
//左
traversal(tree->left);
//中
//第一个节点
if(pre == NULL) {
count = 1;
}else if(pre->val == tree->val) {
count ++;
}else {
count = 1;
}
pre = cur;
if(count == maxCount) {
result.push_back(tree->val);
}
if(count > maxCount) {
maxCount = count;
result.clear();
result.push_back(tree->val);
}
cur = cur-right;
}
}
return result;
}
二叉树最近的公共祖先
TreeNode* lowestCommonAncestor(TreeNode* tree, TreeNode* p, TreeNode* q) {
if(q == tree || p == tree || tree == NULL) return NULL;
TreeNode* left = lowestCommonAncestor(tree->left);
TreeNode* right = lowestCommonAncestor(tree->right);
if(left != NULL && right != NULL) return tree;
if(left == NULL && right != NULL) return right;
else if(left != NULL && right == NULL) return left;
else if(left == NULL && right == NULL) return NULL;
}
二叉搜索树最近的公共祖先
TreeNode* traversal(TreeNode* tree, TreeNode* p, TreeNode* q) {
if(tree == NULL) return tree;
//从左开始遍历
if(tree->val > p->val && tree->val > q->val) {
TreeNode* left = traversal(tree->left);
if(left != NULL) {
return left;
}
}
//从右开始遍历
if(tree->val < p->val && tree->val < q->val) {
TreeNode* right = traversal(tree->right);
if(right != NULL) {
return right;
}
}
//处在中间范围内的节点
return tree;
}
迭代法
TreeNode* lowestCommonAncestor(TreeNode* tree, TreeNode* p, TreeNode* q) {
while(tree != NULL) {
if(tree->val > p->val && tree->val > q->val) {
tree = tree->left;
}else if(tree->val < p->val && tree->val < q->val) {
tree = tree->right;
}else {
return tree;
}
}
return NULL;
}
二叉搜索树的插入操作
递归法
(有返回值)
TreeNode* traversal(TreeNode* tree, int val) {
//结束条件
if(tree == NULL) {
TreeNode* node = new TreeNode(val);
return node;
}
//判断值是否大于或是小于来决定遍历方向,并直接添加节点
if(tree->val > val) tree->left = traversal(tree->left, val);
if(tree->val < val) tree->right = traversal(tree->right, val);
//返回原节点
return tree;
}
(无返回值)
class Solution {
public:
TreeNode* parent;
void traversal(TreeNode* tree, int val) {
if(tree == NULL) {
TreeNode* node = new TreeNode(val);
if(val > parent->val) parent->right = node;
else parent->left = node;
return ;
}
//记录当前的节点,作为下一节点的父节点
parent = tree;
if(tree->val > val) traversal(tree->left, val);
else if(tree-val < val) traversal(tree->right, val);
return ;
}
TreeNode* insertIntoBST(TreeNode* tree, int val) {
parent = new TreeNode(0);
if(tree == NULL) {
TreeNode* newNode = TreeNode(val);
}
traversal(tree, val);
return tree;
}
}
迭代法
TreeNode* insertIntoBST(TreeNode* tree) {
if(tree == NULL) {
TreeNode* node = new TreeNode(val);
return node;
}
TreeNode* cur = tree;
//记录上一个节点
TreeNode* parent = tree;
while(cur != NULL) {
parent = cur;
if(cur->val > val) cur = cur->left;
else if(cur->val < val) cur = cur->right;
}
//到空节点,定义一个新的节点
TreeNode* node = new TreeNode(val);
if(val > parent->val) parent->right = node;
else if(val < parent->val) parent->left = node;
return node;
}
删除二叉搜索树的节点
有以下五种情况:
- 第一种情况:没找到删除的节点,遍历到空节点直接返回了
- 找到删除的节点
- 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
- 第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
- 第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
- 第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点。
迭代法
TreeNode* deleteNode(TreeNode* tree, int key) {
if(tree == NULL) return tree;
if(tree->val ==key) {
//左右孩子都为空
if(tree->left == NULL && tree->right == NULL) {
delete tree;
}
//左节点为空
else if(tree->left == NULL && tree->right != NULL) {
TreeNode* temp = tree;
delete temp;
return tree;
}
//右节点为空
else if(tree->right != NULL && tree->left == NULL) {
TreeNode* temp = tree;
delete temp;
return tree;
}
//左右节点都不为空
else {
TreeNode* cur = tree->right;
while(cur->left != NULL) {
cur = cur->left;
}
cur->left = tree->left;
tree = tree->right;
TreeNode* temp = tree;
delete temp;
return tree;
}
}
if(tree->val > key) tree-left = traversal(tree->left);
if(tree->val < key) tree->right = traversal(tree->right);
return tree;
}
修剪二叉搜索树
给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根节点。
TreeNode* trimBST(TreeNode* tree, int L, int R) {
if(tree == NULL) return tree;
if(tree->val > R) {
TreeNode* left = traversal(tree->left);
return left;
}
if(tree->val < L) {
TreeNode* right = traversal(tree->right);
return right;
}
tree->left = traversal(tree->left);
tree->right = traversal(tree->right);
return tree;
}
迭代法
因为二叉搜索树的有序性,不需要使用栈模拟递归的过程。
在剪枝的时候,可以分为三步:
- 将root移动到[L, R] 范围内,注意是左闭右闭区间
- 剪枝左子树
- 剪枝右子树
TreeNode* trimBST(TreeNode* tree, int L, int R) {
if(tree == NULL) return NULL;
//将节点移动到[L, R] 范围内
while(tree != NULL && (tree->val < L || tree->val > R)) {
if(tree->val > L) tree = tree->left;
else tree = tree->right;
}
//修剪左子树
TreeNode* cur = tree;
while(cur != NULL) {
while(cur->left != NULL && cur->left->val < L) {
cur->left = cur->left->right;
}
cur = cur->left;
}
//恢复当前节点
cur = tree;
//修剪右子树
while(cur != NULL) {
while(cur->right != NULL && cur->right->val > L) {
cur->right = cur->right->left;
}
cur = cur->right;
}
return tree;
}
将有序数组转换为二叉搜索树
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
class Solution {
private:
TreeNode* traversal(vector<int> nums, int left, int right) {
if(left > right) return NULL;
int mid = left + ((left + right) / 2);
TreeNode* newNode = TreeNode(nums[mid]);
newNode->left = traversal(nums, left, mid - 1);
newNode->right = traversal(nums, mid + 1, right);
return newNode;
}
public:
TreeNode* sortedArrayToBST(vector<int> nums) {
TreeNode* node = traversal(nums, 0, nums.size() - 1);
return node;
}
}
迭代法
TreeNode* sortedArrayToBST(vector<int> nums) {
if(nums.size() == 0) return NULL;
//创建一个节点
TreeNode* node = new TreeNode(0);
//创建三个队列,存放新创建的节点,左数组区间,和右数组区间
queue<TreeNode*> nodeQ;
queue<int> leftQ;
queue<int> rightQ;
nodeQ.push(node);
leftQ.push(0);
rightQ.push(nums.size() - 1);
while(! nodeQ.empty()) {
TreeNode* cur = nodeQ.front();
nodeQ.pop();
int left = leftQ.front();
leftQ.pop();
int right = rightQ.front();
rightQ.pop();
int mid = left + ((left + right) / 2);
//给节点赋值
node->val = nums[mid];
//处理左边的节点
if(left < mid - 1) {
node->left = new TreeNode(0);
nodeQ.push(node->left);
leftQ.push(left);
rightQ.push(mid - 1);
}
//处理左边的节点
if(right > mid + 1) {
node->right = new TreeNode(0);
nodeQ.push(node->right);
leftQ.push(mid + 1);
rightQ.push(right);
}
}
return node;
}
把二叉搜索树转换为累加树
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
我们需要反中序遍历这个二叉树,然后顺序累加就可以了。
class Solution {
private:
int pre;
void traversal(TreeNode* node) {
if(node == NULL) return ;
//反中序遍历
traversal(node->right);
node->val += pre;
pre = node->val;
treversal(node->left);
}
public:
TreeNode* convertBST(TreeNode* tree) {
pre = 0;
traversal(tree);
return tree;
}
}
迭代法
TreeNode* convertBST(TreeNode* tree) {
int pre = 0;
if(tree == NULL) return tree;
stack<int> st;
TreeNode* cur = tree;
while(cur != NULL && ! st.empty()) {
if(cur != NULL) {
st.push(cur);
cur = cur->right;
}else {
cur = st.top();
st.pop();
cur->val += pre;
pre = cur->val;
cur = cur->right;
}
}
return tree;
}
- 涉及到二叉树的构造,无论普通二叉树还是二叉搜索树一定前序,都是先构造中节点。
- 求普通二叉树的属性,一般是后序,一般要通过递归函数的返回值做计算。
- 求二叉搜索树的属性,一定是中序了,要不白瞎了有序性了。
注意在普通二叉树的属性中,我用的是一般为后序,例如单纯求深度就用前序,[二叉树:找所有路径 ]也用了前序,这是为了方便让父节点指向子节点。